***이 스레는 통계학에 접한 적이 없는 일반 성인 전용으로 만든 것이어, 일부의 특수한 분들은 대상외로 하겠습니다.또 정확함을 그만큼 우선하고 있지 않았기 때문에, 확실히 공부하고 싶은 사람은 교과서를 사 읽는 것을 추천 합니다.***
6면체의 주사위를 60회 날렸는데 1의 눈이 12회 나왔다고 한다.
아시는 통과해, 주사위의 1의 눈이 나오는 확률은1/6이어, 이론적으로는 주사위를 60회 날리면 10회 정도 1의 눈이 나온다.
이것을 근거로 하면, 12회라고 하는 결과는 타당한 수치이다고 말할 수 있지만, 1의 눈이 30회에 충분해 2 회 밖에가 아니거나 했을 경우는 1의 눈이 나오는 확률이1/6는 아닐지도 모른다는, 의혹이 생긴다.
그림으로 하는 곳 인 느껴
이론치라고 관측치가 가까우면, 이론치를 이끈 법칙이라고 관측치를 이끈 법칙이 같다라고 추정할 수 있지만, 크게 어긋나 있다면 관측치는 이론치를 이끈 법칙에 따라서 않다고 하는 것이 된다.
이 경우,
어느 관측치가 주어진 법칙에 따라서 있는지 어떤지
(을)를 검정하기 위해서 통계학이 사용되는 것이다.
그런데, 확률1/6의 사상이 60회중 N회생확률을 요구하세요, 라고 하는 문제는 실제로 계산하는 것은 귀찮지만 고교생이나, 조금 영리한 중학생이라도 풀 수 있다.아니, 나에게는 풀 수 없어, 는 분은 학교에서 그런 것을 배운 기억이 남아 있으면 오케이입니다.
실제로 60회중 N회 1째가 나오는 회수의 확률을 계산하면 이하와 같은 그래프가 된다.
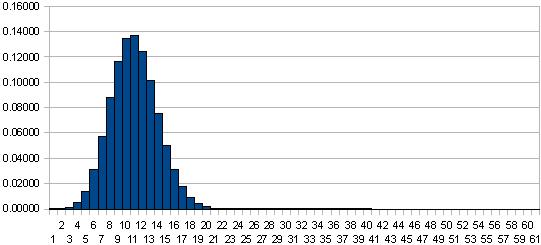
횡축이 1의 눈이 나오는 회수, 세로축이 그 확률이다.
예를 들면 1의 눈이 연속 60회 나오는 확률도 0은 아니라고 하는 것에 주의했으면 좋겠다.
이 그래프에 의하면 1의 눈이 10회 나오는 확률은 13.7%
9회~11회의 범위에 들어가는 확률은 13.4 + 13.7 + 12.5 = 39.6%
그리고 대략95%의 확률로 5회부터 15회의 범위에 안정되는이라고 하는 것을 알 수 있다.
그러니까 2 회 밖에가 아니었다, 라든지 30회 나왔다든가는, 그 95%의 범위외, 5%이하의 확률로 밖에 생기지 않는 드문 현상이다고 말할 수 있어 역시 이것은 이상하지-의, 라는 것이 된다.
그런데, 지금까지는 있는 사상이 생기는 법칙이 기존인 경우, 주사위를 흔들면1/6으로 1의 눈이 나오는 것을 알 수 있고 있는 경우의 이야기이다.여기서 이 주사위가 6면체이다고 하는 전제를 제거해 보기로 한다.한층 더 일반화하고, 확률 p로 1의 눈이 나오기로 한다.6면체라면 p = 0.1666… = 1/6 인 것에 주의해 주세요.
여기서의 통계학의 목적은
1의 눈이 나오는 확률을 추정한다
바꾸어 말하면
관측치로부터 그 관측치를 이끈 법칙을 복원한다
일에 있다.
그리고, 여기서 문제
주사위를 600회 날렸는데 1의 눈이 110회 나왔다.이 관측치로부터 1의 눈이 나오는 확률을 통계적으로 추정해 주세요.
예를 들면 p = 1/6 (6면체의 주사위)이었다고 하는 곳의 관측치는 타당할 것일까.
거기서 조금 전의 그래프를 한번 더 만들어 본다.
(2).jpg)
자세한 계산은 생략하지만, 그저 타당할 것이라고 말하는 결론을 얻을 수 있다.
이것을 0 < p < 1에 관해서 일일이 상세하게 반복해 가면 좋지만, 실제는 그런 일을 하지 않고, p = 110(회)/600(회)로서 그래프를 만들어, 그 그래프로부터 p의 범위를 요구할 수 있다.
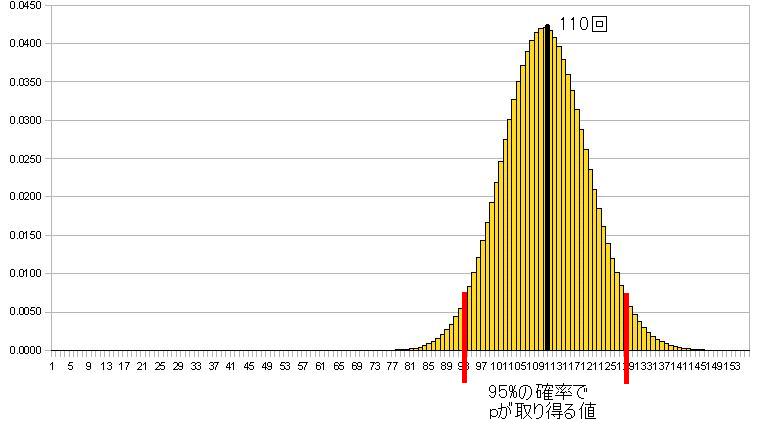
그리고, 이 그래프로부터95%의 확률로 600 * p(1의 눈이 나오는 회수)는 92회부터 128회의 사이에 안정된다고 하는 것을 알 수 있어, 600 * p = 110 ± 18,
p = 0.183 ± 0.030 (95% 신뢰 구간),
뭐15%에서21%의 사이다, 라고 하는 대답을 얻을 수 있다.
그런데, 실은 위의 그래프는 이항 분포라고 하는 확률 분포를 기초로 해 만들어지고 있다.이항 분포가 몰라요 사람은 wiki로 검색해 보자.
현실에 대해서는, 어느 사상이 어떠한 분포에 따라서 있는지, 라고 하는 것이 미지인 것이 많아, 그러한 경우, 위와 같은 방법으로 그래프를 만들고 확률을 구한다고 하는 작업이 원래 할 수 없다.
우선 최초로 보통 주사위와 456새 중 어느 쪽인지 한편을 선택해 그것을 60회 날렸습니다, 라고 시행이라면, 1회만의 결과에서는 아무것도 말할 수 없지요.
여기서 제일 최초로 가리킨, 6면체의 주사위를 60회 날렸을 때의 1의 눈이 나오는 회수의 그래프를 한번 더 보자.

1의 눈이 10회 나오는 확률은 대개14%이다.이것은
주사위를 60회 날리는 작업 * 100회
갔을 경우, 대개 14회는(1의 눈이 10회)이라고 하는 결과를 얻을 수 있는 일을 나타내고 있다.
무엇을 말하고 싶은가 하면 , 시행 회수를 늘리는 것으로, 분포의 형태를 재현 할 수 있다는 것.
하나의 관측치에서는, 그것이 이론치와 얼마나 떨어져 있는지라든가의 정보는 얻을 수 없지만, 복수 모이는 것으로, 이론치를 복원할 수 있다.
그리고, 실제로 난수를 생성하고, 주사위의 1의 눈이 나오는 회수를 시뮬레이션 한 것이 이것↓
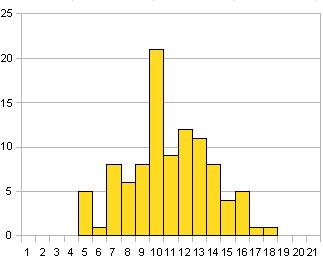
시행 회수 100회
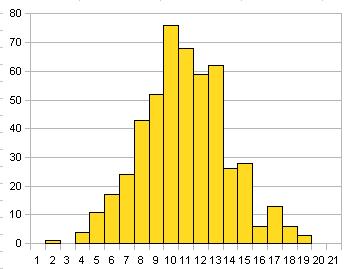
시행 회수 500회
이런 덜컹덜컹의 그래프로 무엇을 알 수 있는 것, 은 사람이 있을지도 모르지만, 거기에 통계학의 진수가 있습니다.시행 회수가 증가하면 증가할수록, 분포는 정규 분포에 수렴 해 나간다고 하는 수학적인 진리가 있어서,…
아, 따로 이해할 필요는 없어요.
시행 회수를 늘리면 대체로 이런 형태에 침착해서 갑니다.
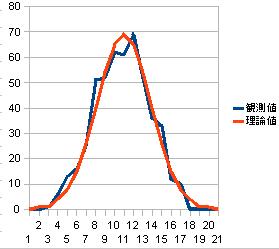
일부러 몇번이나 반복하는 것은,푸른 선의 관측치로부터 공창 지역의 이론치를 복원하는유익입니다.
정규 분포등의 분포는 그 성질이 매우 사용하기 쉬운(정규 분포 이외에도 사용하기 쉬운 분포는 복수 존재한다) 것으로, 평균치나 분산의 평가가 가능하게 되어, 여러가지 통계적 비교에 이용할 수 있습니다.바꾸어 말하면, 다른 분포에 옮겨놓아도 비교는 할 수 없어는 일.
덧붙여서 다항식 근사는의를 모식도로 하는 곳 인 느껴
이론치의 면적이든지 반경이든지를 알고 싶은 정보로 하면, 관측치를 정확하게 트레이스 했을 뿐의 다항식 근사에서는 그러한 정보는 얻을 수 없다.생 데이터 쪽이 더해.
그런데, 정규 분포의 형태를 알면, 나머지는 얼마나의 범위를 설정하면 확률 95%이상이 되는지를 계산할 뿐입니다.거기서 정규 분포의 형태를 알 필요가 있습니다만, 실은 생의 데이터로부터
평균치와표준 편차
(을)를 요구하는 것으로 곧바로 형태가 정해집니다.
실제로 계산하면
평균이 9.89 (60회 주사위를 흔들면 9.89회 1의 눈이 나온다) (이론치는 물론 10)
표준 편차가 2.99(이론치가 2.89)
된다.
세세한 계산은 생략하기로 하고, 대체로 60회 주사위를 흔들면 1의 눈이 나오는 회수는 5회부터 15의 범위에 들어가라는 결론을 얻을 수 있다.
좀 더 오차라든지 검정의 이야기를 하는 것이 좋지만 이번은 여기까지.
***このスレは統計学に触れたことのない一般成人向けに作ったものであり、一部の特殊な方たちは対象外とさせていただきます。また正確さをそれほど優先していないので、しっかり勉強したい人は教科書を買って読むことを推奨します。***
六面体のサイコロを60回ふったところ1の目が12回出たとする。
ご存知のとおり、サイコロの1の目が出る確率は1/6であり、理論的にはサイコロを60回ふれば10回程度1の目が出る。
このことを踏まえれば、12回と言う結果は妥当な数値であると言えるが、1の目が30回でたり、2回しかでなかったりした場合は1の目が出る確率が1/6ではないかもしれない、という疑惑が生じる。
図にするとこんな感じ
理論値と観測値が近ければ、理論値を導いた法則と観測値を導いた法則が同じであると推定できるが、大きくずれているなら観測値は理論値を導いた法則に従っていないということになる。
この場合、
ある観測値が与えられた法則にしたがっているかどうか
を検定するために統計学が使用されるのである。
さて、確率1/6の事象が60回中N回生じる確率を求めなさい、という問題は実際に計算することは面倒だが高校生や、ちょっと賢い中学生でも解くことができる。いや、俺には解けないよ、って方は学校でそういうことを習った記憶が残っていればオッケーです。
実際に60回中N回1目がでる回数の確率を計算すると以下のようなグラフとなる。

横軸が1の目が出る回数、縦軸がその確率である。
例えば1の目が連続60回出る確率も0ではないと言うことに注意して欲しい。
このグラフによれば1の目が10回出る確率は13.7%
9回~11回の範囲に収まる確率は13.4 + 13.7 + 12.5 = 39.6%
そしておよそ95%の確率で5回から15回の範囲におさまると言うことがわかる。
だから2回しかでなかった、とか30回出たとかは、その95%の範囲外、5%以下の確率でしか生じない珍しい現象であると言え、やっぱこれはおかしいんじゃねーの、ということになる。
さて、これまではある事象が生じる法則が既知である場合、サイコロを振ったら1/6で1の目が出ることがわかっている場合の話である。ここでこのサイコロが六面体であるという前提を取り去ってみることにする。さらに一般化して、確率pで1の目が出ることにする。6面体ならp = 0.1666… = 1/6 であることに注意してください。
ここでの統計学の目的は
1の目が出る確率を推定する
言い換えると
観測値からその観測値を導いた法則を復元する
ことにある。
で、ここで問題
サイコロを600回ふったところ1の目が110回出た。この観測値から1の目が出る確率を統計的に推定しなさい。
例えばp = 1/6 (六面体のサイコロ)であったとするとこの観測値は妥当だろうか。
そこで先程のグラフをもう一度作ってみる。
(2).jpg)
詳しい計算は省くが、まあまあ妥当だろうと言う結論が得られる。
これを 0 < p < 1に関して逐一繰り返していけばいいのだが、実際はそんなことをせず、p = 110(回)/600(回)としてグラフを作り、そのグラフからpの範囲を求めることができる。

で、このグラフから95%の確率で600 * p(1の目が出る回数) は92回から128回の間におさまると言うことがわかり、600 * p = 110 ± 18、
p = 0.183 ± 0.030 (95%信頼区間)、
まあ15%から21%の間だな、と言う答えを得ることができる。
さて、実は上のグラフは二項分布と言う確率分布をもとにして作られている。二項分布がわからん人はwikiで検索してみようね。
現実においては、ある事象がどのような分布に従っているか、と言うことが未知であることが多く、そのような場合、上のような方法でグラフを作って確率をもとめると言う作業がそもそもできない。
まず最初に普通のサイコロと456賽のうちどちらか一方を選んでそれを60回ふりました、て試行なら、1回だけの結果からはなんにも言えないでしょ。
ここで一番最初に示した、6面体のサイコロを60回ふった時の1の目が出る回数のグラフをもう一度見てみよう。

1の目が10回でる確率は大体14%である。これは
サイコロを60回振る作業 * 100回
行った場合、大体14回は(1の目が10回)と言う結果が得られる事を示している。
何が言いたいかというと、試行回数を増やすことで、分布の形を再現出来るってこと。
ひとつの観測値では、それが理論値とどれだけ離れているかとかの情報は得られないが、複数集まることにより、理論値を復元できる。
で、実際に乱数を生成して、サイコロの1の目が出る回数をシミュレーションしたものがこれ↓

試行回数100回

試行回数500回
こんなガタガタのグラフで何がわかるの、って人がいるかも知れないけど、そこに統計学の真髄があります。試行回数が増えれば増えるほど、分布は正規分布に収斂していくという数学的な真理がありまして、…
あ、別に理解する必要はないですよ。
試行回数を増やせばだいたいこんな形に落ち着いていきます。

わざわざ何回も繰り返すのは、青線の観測値から赤線の理論値を復元するためです。
正規分布などの分布はその性質が非常に使いやすい(正規分布以外にも使いやすい分布は複数存在する)ので、平均値や分散の評価が可能になり、様々な統計的比較に用いることができます。言い換えると、他の分布に置き換えても比較なんてできないよってこと。
ちなみに多項式近似ってのを模式図にするとこんな感じ
理論値の面積なり半径なりが知りたい情報とすると、観測値を正確にトレースしただけの多項式近似ではそれらの情報は得られない。生データのほうがまし。
さて、正規分布の形がわかれば、あとはどれだけの範囲を設定すれば確率95%以上となるかを計算するだけです。そこで正規分布の形を知る必要がありますが、実は生のデータから
平均値と標準偏差
を求めることですぐに形が決まります。
実際に計算すると
平均が9.89 (60回サイコロを振れば9.89回1の目が出る) (理論値はもちろん10)
標準偏差が2.99(理論値が2.89)
となる。
細かい計算は省くことにして、だいたい60回サイコロを振ると1の目が出る回数は5回から15の範囲に収まるよって結論が得られる。
もうちょっと誤差とか検定の話をした方がいいんだが今回はここまで。

