생선회의 의미불명한 이론은 접어두고, 재미있는 경향이 발견되었으므로
.jpg)
/jp/exchange/photo/read.php?uid=3299&fid=3299&thread=1000000&idx=1&page=2&tname=exc_board_14&number=1999
보다.이하의 그래프는 쇼와 5년 조선에서 행해진 국세조사의 데이터에 근거하고 있습니다.
어쩐지 구부러져 보이는 사람이 있는 것 같지만, 쫙 본 느낌 지수함수적(y = a ^ x)인 그래프로 보인다.
지수함수라고 하는 것은 예를 들어 인구 1만명으로 매년10% 두개인구가 증가해 나가면, n년 후에는 몇 사람이 되겠지요
그렇다고 할 때 이용할 수 있는 함수로, 이 나라의 3년 후의 인구는 10000 * 1.10 * 1.10 * 1.10 = 13310명이 된다.
이 지수함수는 곡선이므로 구부러지는 것이 당연하고, 기울기가 다르다!(이)라고 외쳐도 무슨 발견으로도 되지 않습니다.
덧붙여서 매년 100만명 태어나 1년에 그10%가 죽어 가면 가정했을 때의 생선회 곡선이 이것↓
.jpg)
당연히 출생수와 사망률이 일정이므로 인구의 변화는 전혀 일어나지 않지만, 젊은층과 성인 이후에 기울기는 다르다.
일단 생선회용으로 증가수(n재주꾼구-n+1 재주꾼구)의 그래프를 만들었기 때문에 실어 둔다
.jpg)
당연, 증가수(기울기를 보는 것과 같아)를 보는 것으로 얻을 수 있는 정보는 거의 없다.
왜냐하면 있는 세대의 인구가 많으면 많을수록, 증가수나 감소수도 많아지므로,
그 세대의 인구로 보정할 필요가 있다.
이것을 봐 아직 증가 경향을 읽어낼 수 있다면 의사에게 가는 편이 좋다.안과의사가 아니고 머리 쪽.
그리고, 이런 일은 아무래도 좋아서, 무엇이 재미있는가 하면 , 지수함수적인 그래프(y = a ^ x)라고 하는 것은 a( = n세/n+1세)가
일정한다는 것을 의미하고 있고, 이것은 출생수가 일정이라고 하면, 사망률이 일정이라는 것이 된다.
주지대로 이 시대는 젊은층의 사망률은 성인의 그것보다 약간인가 높다.
즉 사망률 일정이라고 하는 것은 있을 수 없기 때문에, 출생수가 매년 증가하고 있다고 하는 것이 된다.응.
그리고, 그 매년의 증가율(?)(이)가 이것.
세로축은(n세의 인구)/(n+1세의 인구)를 나타내고 있어 변화가 없으면 1이 된다.
.jpg)
노인은 당연히 사망률이 높기 때문에, 증가율은 조금 비싸게 되어 있다.(80세의 인구)/(81세의 인구)가 높은 것은
당연하네요.1년에 비교적 많은 분이 없어지므로 분모가 작아집니다.
그렇게 말한 변두리값을 제외하면 놀랄 만한 일로 증가율(?)(은)는 거의 일정이 되고 있다.즉 젊은층의 높은 사망률
(을)를 많은 다하는 만큼 출생수가 증가하고 있다고 결론 붙일 수 있는 것은 아닐까요.
물론, 이것이 타국과 라고 어떤가라고 하는 비교는 필요합니다만.
그런데, 여기서 증가율이 일정이라고 하는 가설을 검증하기 위해(때문에), 지수함수로 근사 곡선을 써 봅시다.
60세 이상과 0세는 쫙 보고 빗나가 값이므로 제외해 있습니다.
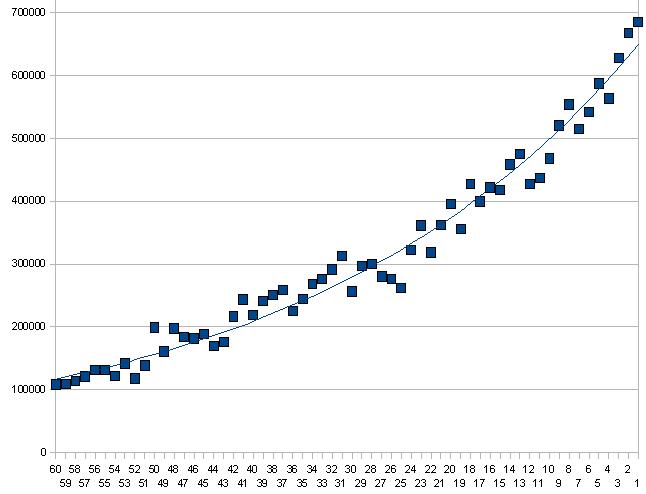
압도적이지 않은지, 우리 그래프는 w
刺身の意味不明な理論はさておいて、面白い傾向が見つかったので
.jpg)
より。以下のグラフは昭和5年 朝鮮で行われた国勢調査のデータに基づいております。
なんか曲がって見える人がいるらしいけど、ぱっと見た感じ指数関数的(y = a ^ x)なグラフに見える。
指数関数ってのはたとえば人口1万人で毎年10%ずつ人口が増加していけば、n年後には何人になるでしょう
というときに用いることができる関数で、この国の3年後の人口は10000 * 1.10 * 1.10 * 1.10 = 13310人となる。
この指数関数は曲線なので曲がって当然であり、傾きが違う!と叫んでも何の発見にもなりません。
ちなみに毎年100万人生まれて1年でその10%が死んでいくと仮定したときの刺身曲線がこれ↓
.jpg)
当然出生数と死亡率が一定なので人口の変化はまったくおきないが、若年層と成人以後で傾きは異なる。
一応刺身用に増加数(n才人口-n+1才人口)のグラフを作ったんで載せておく
.jpg)
当然、増加数(傾きを見ることと同じだよ)を見ることで得られる情報はほとんどない。
なぜならある世代の人口が多ければ多いほど、増加数や減少数も多くなるので、
その世代の人口で補正する必要がある。
これを見てまだ増加傾向が読み取れるんなら医者に行ったほうがいい。目医者じゃなくて頭のほうな。
で、こんなことはどうでもよくて、何が面白いかというと、指数関数的なグラフ(y = a ^ x)ということはa( = n才/n+1才)が
一定であるってことを意味していて、これは出生数が一定だとすると、死亡率が一定ということになる。
周知のとおりこの時代は若年層の死亡率は成人のそれよりも幾分か高い。
つまり死亡率一定ということはありえないので、出生数が毎年増加しているということになる。うん。
んで、その年毎の増加率(?)がこれ。
縦軸は(n才の人口)/(n+1才の人口)をあらわしており、変化がないなら1となる。
.jpg)
老人は当然死亡率が高いので、増加率は高めになっている。(80才の人口)/(81才の人口)が高いのは
当然ですよね。1年で比較的多くの方がなくなるので分母が小さくなります。
そういった外れ値を除けば驚くべきことに増加率(?)はほぼ一定となっている。すなわち若年層の高い死亡率
を多い尽くすほど出生数が増加していると結論付けることができるのではないでしょうか。
もちろん、これが他国とくれべてどうなのかという比較は必要ですが。
さて、ここで増加率が一定と言う仮説を検証するため、指数関数で近似曲線を書いてみましょう。
60歳以上と0歳はぱっと見て外れ値なので除いてあります。

圧倒的じゃないか、我がグラフはw

