http://ameblo.jp/s-ediy-ware-house/entry-10821296144.html
жҠңзІӢгҒ—гҒҰгҒҝгҒҫгҒ—гҒҹгҖҖпҪ—
гҖҗе•ҸйЎҢв‘ҰгҖ‘
гҒӮгҒӘгҒҹгҒҜеҗҢгҒҳгӮөгӮӨгӮәгҒ®гғңгғјгғ«гӮ’8гҒӨгӮӮгҒЈгҒҰгҒ„гҒҫгҒҷгҖӮ
гҒқгҒ®гҒҶгҒЎ7гҒӨгҒҜеҗҢгҒҳйҮҚгҒ•гҒ§гҒҷгҒҢгҖҒ1гҒӨгҒҜгҒ»гҒӢгҒ®гӮӮгҒ®гӮҲгӮҠгӮӮгӮҸгҒҡгҒӢгҒ«йҮҚгҒ„гҒ§гҒҷгҖӮ
з§ӨгӮ’2еӣһгҒ гҒ‘дҪҝгҒЈгҒҰгҒ“гҒ®гӮҸгҒҡгҒӢгҒ«йҮҚгҒ„гғңгғјгғ«гӮ’иҰӢгҒӨгҒ‘гӮӢгҒ«гҒҜгҒ©гҒҶгҒҷгӮҢгҒ°гҒ„гҒ„гҒ§гҒҷгҒӢпјҹ
пјҲеғ•гҒ®еӣһзӯ”пјү
1еӣһзӣ®гҒҜ3еҖӢvs3еҖӢгҖҒгҒ©гҒЎгӮүгҒӢгҒ«еӮҫгҒ‘гҒ°гҖҒ
гҒқгҒ®3еҖӢгҒ®дёӯгҒ®2еҖӢгӮ’йҒёгӮ“гҒ§2еӣһзӣ®гҖӮ
еӮҫгҒ‘гҒ°гҒқгӮҢгҒҢгҒқгҒ®гғңгғјгғ«гҖӮ
еӮҫгҒӢгҒӘгҒ‘гӮҢгҒ°ж®ӢгҒЈгҒҹ1еҖӢгҖӮ
жңҖеҲқгҒ®3еҖӢvs3еҖӢгҒ§еӮҫгҒӢгҒӘгҒ‘гӮҢгҒ°гҖҒ
ж®ӢгҒЈгҒҹ2гҒӨгҒ§2еӣһзӣ®гҖӮ
гҒ“гҒ®е•ҸйЎҢгҒҜгҖҒгӮ¬гғғгғ„гғӘй ӯгҒ®дҪ“ж“ҚгҒҝгҒҹгҒ„гҒӘж„ҹгҒҳпҪ—(гғ»ВҙР·`гғ»)
гҖҺжЁЎзҜ„и§Јзӯ”гҖҸ
в‘ .3еҖӢгҒЁ3еҖӢгӮ’з§ӨгҒ§жҜ”гҒ№гӮӢгҖӮ
в‘Ў.в‘ гҒ®зөҗжһңгҖҒгҒ„гҒҡгӮҢгҒӢгҒ®зҡҝгҒҢйҮҚгҒ‘гӮҢгҒ°гҖҒгҒқгҒ®3гҒӨгҒ®гҒҶгҒЎд»»ж„ҸгҒ®2гҒӨгӮ’з§ӨгҒ§жҜ”гҒ№гҖҒ
гғ»гҒ©гҒЎгӮүгҒӢгҒҢйҮҚгҒ‘гӮҢгҒ°гҖҒгҒқгӮҢгҒҢгҖҢгӮҸгҒҡгҒӢгҒ«йҮҚгҒ„гғңгғјгғ«гҖҚгҖӮ
гғ»зӯүгҒ—гҒ‘гӮҢгҒ°гҖҒжҜ”гҒ№гҒӘгҒӢгҒЈгҒҹж®ӢгӮӢ1гҒӨгҒҢгҖҢгӮҸгҒҡгҒӢгҒ«йҮҚгҒ„гғңгғјгғ«гҖҚгҖӮ
в‘ў.в‘ гҒ®зөҗжһңгҖҒз§ӨгҒҢзӯүгҒ—гҒ‘гӮҢгҒ°гҖҒж®ӢгӮӢ2гҒӨгӮ’жҜ”гҒ№йҮҚгҒ„ж–№гҒҢгҖҢгӮҸгҒҡгҒӢгҒ«йҮҚгҒ„гғңгғјгғ«гҖҚгҖӮ
гғ»гғ»гғ»гҒ гҒқгҒҶгҒ§гҒҷгҖҖпјҫпјҫ
гҒӨгҒ„гҒ§гҒ«гғ»гғ»гғ»гҒ“гӮ“гҒӘгҒ®гӮӮгҒӮгӮӢгӮҲгҒҶгҒ§гҒҷгҖҖпҪ—пҪ—пҪ—пҪ—пҪ—
гҖҗе•ҸйЎҢв‘ЎгҖ‘
гҖҺжӯЈ20йқўдҪ“гӮ’дёүиүІгҒ§еЎ—гӮҠеҲҶгҒ‘гҒ—гҒҰгҒ„гҒЈгҒҹе ҙеҗҲгҖҒдҪ•йҖҡгӮҠгҒ®гғ‘гӮҝгғјгғігҒҢеҮәгҒҚгӮӢгҒӢгҖҸ
пјҲеғ•гҒ®зӯ”гҒҲпјү
дҫӢгҒҲгҒ°гҖҒ
иөӨгғ»йқ’гғ»з·‘гҒ®дёүиүІгҒҢгҒӮгӮӢгҒЁгҒ—гҒҰгҖҒеҗҢгҒҳиүІгҒ°гҒӢгӮҠгӮ’еЎ—гӮӢгҖӮ
иөӨгҒ°гҒӢгӮҠеЎ—гӮӢпјҡ1йҖҡгӮҠгҖӮ
йқ’гҒ°гҒӢгӮҠеЎ—гӮӢпјҡ1йҖҡгӮҠгҖӮ
з·‘гҒ°гҒӢгӮҠеЎ—гӮӢпјҡ1йҖҡгӮҠгҖӮ
гҒ—гҒӢгҒ—гҖҒиөӨгҒ гҒ‘дёҖйқўгҒ«еЎ—гӮҠгҖҒгҒқгҒ®д»–гҒҜз·‘гҒ«еЎ—гҒЈгҒҹе ҙеҗҲгҒӘгҒ©гғ»гғ»
зҙ°гҒӢгҒӘгғ‘гӮҝгғјгғігҒ«гҒӘгҒЈгҒҰгҒҸгӮӢгҒЁе…ЁгҒҸеҲҶгҒӢгӮүгҒӘгҒҸгҒӘгҒЈгҒҰгҒҸгӮӢгғ»гғ»гҖӮ
[зҸҚжЁЎзҜ„и§Јзӯ”]вҖ»гғҚгғғгғҲгҒ§жҺўгҒ—гҒҹгӮӮгҒ®w
зү©зҗҶеӯҰиҖ…гҒ§гӮөгӮӨгӮЁгғігӮ№гғ©гӮӨгӮҝгғјгҒ®дәәгҒҢгҖҒпј’ж—Ҙй–“еҫ№еӨңгҒ§иҖғгҒҲгҒҰгҖҒ
дҪ“иӘҝгӮ’еҙ©гҒ—гҒҹгӮҲгҒҶгҒӘгҒ®гҒ§гҒҷгҒҢгғ»гғ»гғ»
гӮ„гҒЈгҒЁзӯ”гҒҲгҒ«гҒҹгҒ©гӮҠзқҖгҒ„гҒҹгӮҲгҒҶгҒ§гҒҷгҖӮ
гҖҖгҖҖгҖҖгҖҖгҖҖгҖҖгҖҖгҖҖгҖҖгҖҖвҶ“
зӯ”гҒҲгҒҜгҖҒпј•пјҳпј‘пј“дёҮпј•пј•йҖҡгӮҠгҒ§гҒҷгҖӮ
гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»гғ»
гҒӣгҒЈгҒӢгҒҸгҒӘгҒ®гҒ§гғ»гғ»гғ»з§ҒгҒӢгӮүе•ҸйЎҢгҖҖпҪ—пҪ—пҪ—
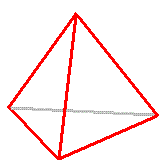
гҖҺжӯЈеӣӣйқўдҪ“гӮ’дёүиүІгҒ§еЎ—гӮҠеҲҶгҒ‘гҒ—гҒҰгҒ„гҒЈгҒҹе ҙеҗҲгҖҒдҪ•йҖҡгӮҠгҒ®гғ‘гӮҝгғјгғігҒҢеҮәгҒҚгӮӢгҒӢгҖҸпјҹ
http://ameblo.jp/s-ediy-ware-house/entry-10821296144.html
л°ңм·Ңн•ҙ ліҙм•ҳмҠөлӢҲлӢӨгҖҖw
гҖҗл¬ём ң⑦гҖ‘
лӢ№мӢ мқҖ к°ҷмқҖ мӮ¬мқҙмҰҲмқҳ ліјмқ„ 8мҢ“мқҙкі мһҲмҠөлӢҲлӢӨ.
к·ё мӨ‘ 7лҠ” к°ҷмқҖ л¬ҙкІҢмһ…лӢҲлӢӨл§Ң, 1к°ңлҠ” лӢӨлҘё кІғліҙлӢӨ мЎ°кёҲ л¬ҙкІҒмҠөлӢҲлӢӨ.
м Җмҡёмқ„ 2нҡҢл§Ң мӮ¬мҡ©н•ҙ мқҙ мЎ°кёҲ л¬ҙкұ°мҡҙ ліјмқ„ м°ҫм•„лӮҙл Өл©ҙ м–ҙл–»кІҢ н•ҳл©ҙ мўӢмҠөлӢҲк№Ңпјҹ
(лӮҳмқҳ нҡҢлӢө)
1нҡҢм§ёлҠ” 3к°ң vs3к°ң, м–ҙл”ҳк°Җм—җ кё°мҡёл©ҙ,
к·ё 3к°ңм•Ҳмқҳ 2к°ңлҘј м„ нғқн•ҙ 2лІҲм§ё.
кё°мҡёл©ҙ к·ёкІғмқҙ к·ё ліј.
кё°мҡём§Җ м•Ҡмңјл©ҙ лӮЁмқҖ 1к°ң.
мөңмҙҲмқҳ 3к°ң vs3к°ңлЎң кё°мҡём§Җ м•Ҡмңјл©ҙ,
лӮЁмқҖ 2лЎң 2лІҲм§ё.
мқҙ л¬ём ңлҠ”, к°“нҠёлҰ¬л‘җмқҳ мІҙмЎ°к°ҷмқҖ лҠҗлӮҢ w(В·вҖІз`В·)
гҖҢлӘЁлІ” н•ҙлӢөгҖҚ
①.3к°ңмҷҖ 3к°ңлҘј м ҖмҡёлЎң 비көҗн•ңлӢӨ.
②.①мқҳ кІ°кіј, лӘҮк°ңмқҳ м ‘мӢңк°Җ л¬ҙкұ°мҡ°л©ҙ, к·ё 3к°ң мӨ‘ мһ„мқҳмқҳ 2к°ңлҘј м ҖмҡёлЎң 비көҗн•ҙ
В·м–ҙлҠҗ мӘҪмқём§Җк°Җ л¬ҙкұ°мҡ°л©ҙ, к·ёкІғмқҙ гҖҢмЎ°кёҲ л¬ҙкұ°мҡҙ ліјгҖҚ.
В·лҸҷмқјн•ҳл©ҙ, 비көҗн•ҳм§Җ м•Ҡм•ҳлӢӨ лӮЁлҠ” 1к°ңк°Җ гҖҢмЎ°кёҲ л¬ҙкұ°мҡҙ ліјгҖҚ.
③.①мқҳ кІ°кіј, м Җмҡёмқҙ лҸҷмқјн•ҳл©ҙ, лӮЁлҠ” 2лҘј 비көҗн•ҙ л¬ҙкұ°мҡҙ кІғмқҙ гҖҢмЎ°кёҲ л¬ҙкұ°мҡҙ ліјгҖҚ.
В·В·В·(мқҙ)лқјкі н•©лӢҲлӢӨгҖҖпјҫпјҫ
н•ҳлҠ” к№Җм—җВ·В·В·мқҙлҹ° кұҙлҸ„ мһҲлҠ” кІғ к°ҷмҠөлӢҲлӢӨгҖҖwwwww
гҖҗл¬ём ң②гҖ‘
гҖҢм • 20л©ҙмІҙлҘј мӮјмғүмңјлЎң л°ңлқј лӮҳлҲ„м–ҙ н•ҳкі к°”мқ„ кІҪмҡ°, лӘҮк°Җм§Җмқҳ нҢЁн„ҙмқҙ м¶ң мҳ¬к№ҢгҖҚ
(лӮҳмқҳ лҢҖлӢө)
мҳҲлҘј л“Өл©ҙ,
м ҒВ·мІӯВ·лЎқмқҳ мӮјмғүмқҙ мһҲлӢӨкі н•ҳм—¬, к°ҷмқҖ мғүл§Ңмқ„ л°”лҘёлӢӨ.
л№Ёк°•л§Ң л°”лҘҙлҠ”пјҡ1л°©лІ•.
нҢҢлһ‘л§Ң л°”лҘҙлҠ”пјҡ1л°©лІ•.
мҙҲлЎқл§Ң л°”лҘҙлҠ”пјҡ1л°©лІ•.
к·ёлҹ¬лӮҳ, л№Ёк°•л§Ң мқјл©ҙм—җ л°ңлқј, к·ё мҷёлҠ” мҙҲлЎқм—җ л°ңлһҗмқ„ кІҪмҡ° л“ұВ·В·
섬세н•ң нҢЁн„ҙмқҙ лҗҳм–ҙ м§Җл©ҙ мҷ„м „нһҲ лӘЁлҘҙкІҢ лҗҳм–ҙ 진лӢӨВ·В·.
[진лӘЁлІ” н•ҙлӢө]вҖ»л„·м—җм„ң м°ҫмқҖ кІғ w
л¬јлҰ¬н•ҷмһҗлЎң мӮ¬мқҙм–ёмҠӨ лқјмқҙн„°мқҳ мӮ¬лһҢмқҙ, 2мқјк°„ мІ м•јлЎң мғқк°Ғн•ҳкі ,
м»Ёл””м…ҳмқ„ л¬ҙл„ҲлңЁлҰ° кІғ к°ҷмҠөлӢҲлӢӨл§ҢВ·В·В·
кІЁмҡ° лҢҖлӢөн•ҙм—җ к°Җк№ҢмҠӨлЎң лҸ„м°©н•ң кІғ к°ҷмҠөлӢҲлӢӨ.
гҖҖгҖҖгҖҖгҖҖгҖҖгҖҖгҖҖгҖҖгҖҖгҖҖвҶ“
лҢҖлӢөмқҖ, 5813л§Ң 55л°©лІ•мһ…лӢҲлӢӨ.
В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·В·
лӘЁмІҳлҹјмқҙлҜҖлЎңВ·В·В·лӮҳл¶Җн„° л¬ём ңгҖҖwww

гҖҢм •мӮ¬л©ҙмІҙлҘј мӮјмғүмңјлЎң л°ңлқј лӮҳлҲ„м–ҙ н•ҳкі к°”мқ„ кІҪмҡ°, лӘҮк°Җм§Җмқҳ нҢЁн„ҙмқҙ м¶ң мҳ¬к№ҢгҖҚпјҹ
������

